
The first and last knot, which we specify manually. Presently I'm generating the query points for that grid, in python, as given below.

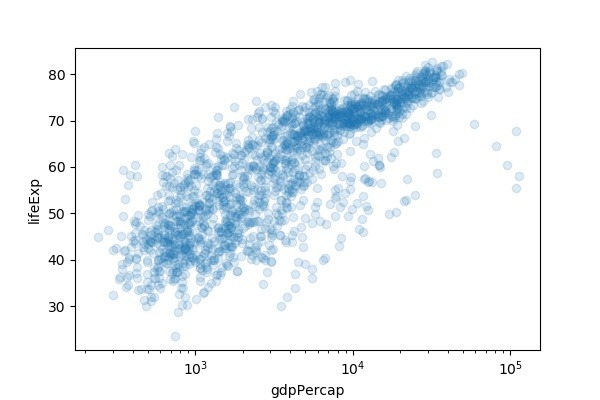
I'm using inverse distance weighting interpolation method to interpolate them in a rectangular grid of pixels. The splines period is the distance between I've got some scattered data in the form of (latitude, longitude, someParameterValue). In the following case we show how periodic splines provide a better fitīoth within and outside of the range of training data given the additional Which have equal function value and equal derivatives at the first and last Such effects can be modelled using periodic splines, with seasonal effects, we expect a periodic continuation of In the previous example we saw the limitations of polynomials and splines forĮxtrapolation beyond the range of the training observations. This extrapolating behaviour could be changed by the argument Every basisįunction has local support and is continued as a constant beyond the fitted To connect these points of scatter plot in order, call (x, y) keeping x and y the same as ones passed into scatter() function.
There for technical reasons, so we refrain from showing them. Call show() After Calling Both scatter() and plot() (x, y) with x as a sequence of x-coordinates and y as a sequence of y-coordinates creates a scatter plot of points. Knots each to the left and to the right of the fitted interval. Note that there are degree number of additional In the right figure, we see the six B-splineīasis functions of degree=3 and also the four knot positions that wereĬhosen during fit. In the left plot, we recognize the lines corresponding to simple monomialsįrom x**0 to x**3. vlines ( knots, ymin = 0, ymax = 0.8, linestyles = "dashed" ) plt. set_title ( "SplineTransformer" ) # plot knots of spline knots = splt. plot ( x_plot, y_plot, label = f "degree " for n in range ( 6 )]) axes. fit ( X_train, y_train ) y_plot = model. scatter ( x_train, y_train, label = "training points" ) # polynomial features for degree in : model = make_pipeline ( PolynomialFeatures ( degree ), Ridge ( alpha = 1e-3 )) model. plot ( x_plot, f ( x_plot ), linewidth = lw, label = "ground truth" ) # plot training points ax. Color to apply to all plot elements will be superseded by colors passed in scatterkws or linekws.
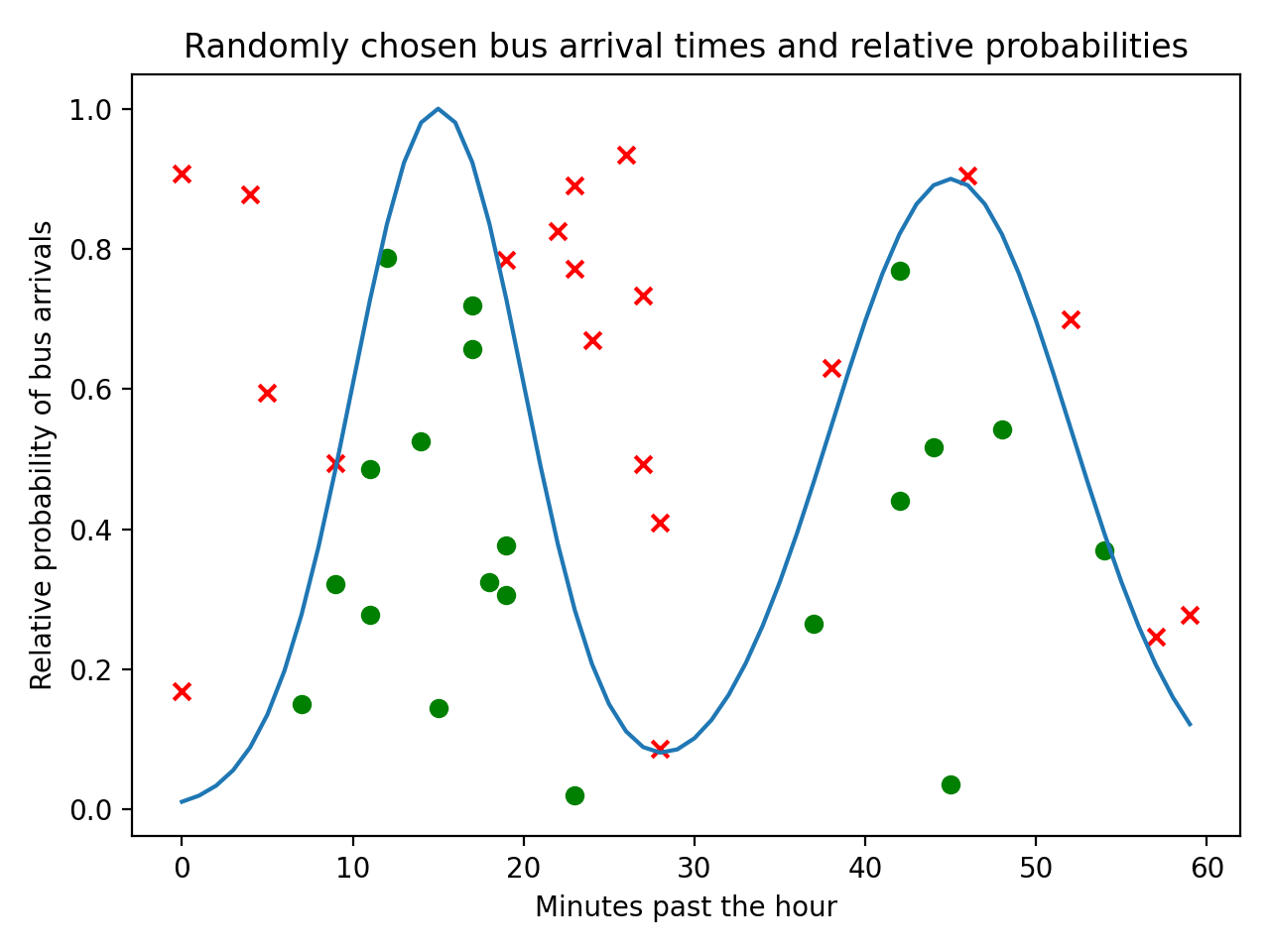
Label to apply to either the scatterplot or regression line (if scatter is False) for use in a legend.
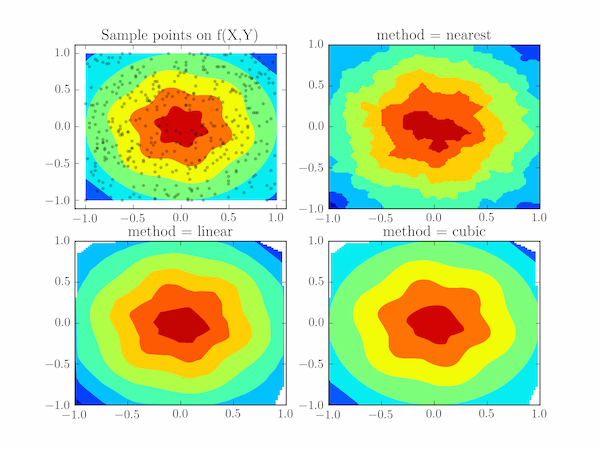
plt.tricontour(x,y,z)Īn example comparing the latter two methods is found on the matplotlib page.# plot function lw = 2 fig, ax = plt. This can be helpful when plotting variables that take discrete values. Zi = griddata((x, y), z, (xi, yi), method='linear')įinally, one can plot a contour completely without the use of a quadrilateral grid. Create a scatter plot using plt.scatter() Use the required and optional input parameters Customize scatter plots for basic and more advanced plots Represent more than two dimensions with plt.scatter() You can get the most out of visualization using plt.scatter() by learning more about all the features in Matplotlib and dealing with data using. In case the data is not living on a quadrilateral grid, one can interpolate the data on a grid. X,y,z = np.loadtxt("data.txt", unpack=True) #x y zĬan plotted as a contour using import matplotlib.pyplot as plt If the x and y data already define a grid, they can be easily reshaped to a quadrilateral grid. The solution will depend on how the data is organized.


 0 kommentar(er)
0 kommentar(er)
