The general term, in terms of π, is therefore equal to two π plus 21. Corbettmaths Videos, worksheets, 5-a-day and much more. Terms of a quadratic sequence can be worked out in the same way. The Corbettmaths Video tutorial on finding the nth term for Quadratic Sequences using method 3. Collecting our like terms, 23 and negative two, gives us 21. The Corbettmaths Video tutorial on finding the nth term for Quadratic Sequences using method 3. The nth term for a quadratic sequence has a term that contains (x2). Intro Quadratic Sequences: nth Term Algebra Maths FuseSchool FuseSchool - Global Education 699K subscribers Subscribe 8.2K views 3 years ago MATHS In this video weβre going to look at. We can distribute the parentheses or expand the brackets by multiplying two by π and two by negative one.
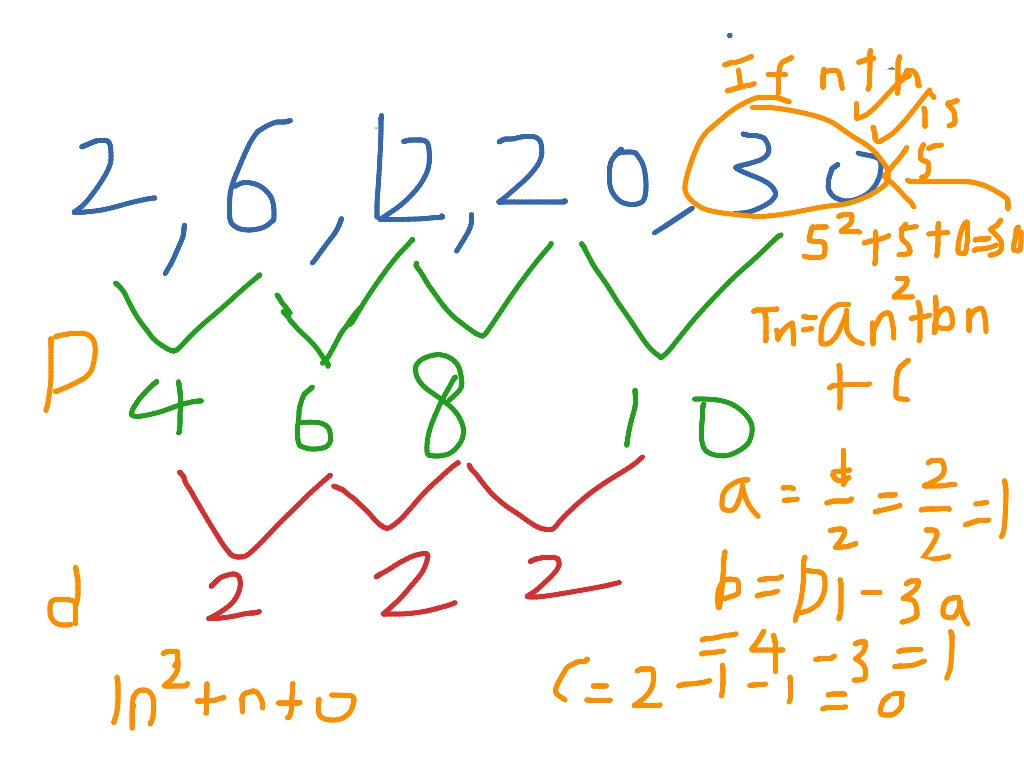
π sub π is therefore equal to 23 plus π minus one multiplied by two. Finding any term in a quadratic sequence using an n th term rule: In any sequence, if you know the n th term rule, you can find any term in that sequence.
As each odd number is two greater than the previous odd number, the common difference π is equal to two. The Nth Term of Quadratic Sequences Maths Genie 103K subscribers 467K views 7 years ago Grade 8/9 Revision GCSE Maths revision tutorial video. π is also sometimes denoted by π sub one. The general term π π of any arithmetic sequence is given by π plus π minus one multiplied by π, where π is the first term in the sequence and π is the common difference. The first five terms of the sequence of all the odd numbers greater than 21 are 23, 25, 27, 29, and 31. The first odd number that is greater than 21 is 23. They end in one, three, five, seven, and nine. Question 13: A sequence has an nth term of n 6n + 7 Work out which term in the sequence has a value of 23. The odd numbers are all the numbers not divisible by two. Question 12: A sequence has an nth term of n + 2n 5 Work out which term in the sequence has a value of 58. Find the first five terms and the general term, in terms of π, of the sequence of all the odd numbers greater than 21. Intro Quadratic Sequences: nth Term Algebra Maths FuseSchool FuseSchool - Global Education 716K subscribers Subscribe 48K views 5 years ago MATHS In this video we look at quadratic.
0 kommentar(er)
